复旦大学数学科学学院高等代数精品课程网站

复旦大学数学类基础课程

《高等代数》教学大纲

MATH120011 高等代数（ I ）学分数5 周学时4+2

总学时96 （讲课64，习题课32）

MATH13000 高等代数（ II ）学分数5 周学时4+2

总学时96 （讲课64，习题32）

一、课程的性质、目的和教学方式

高等代数是数学学院中最重要的数学基础课之一。它以严密的逻辑、系统的推理、抽象的思维作为其特点，其内容包括多种线性系统和结构。是数学系本科一、二年级学生的必修课。本课程总学时为192学时，其中讲课为128学时，习题课为64学时，共分二学期完成，课程名称分别为《高等代数I》，《高等代数II》。通过教学，使学生全面、系统地掌握高等代数的基础知识和代数学的基本思想方法；培养与提高代数的理论分析问题与解决问题的能力；为学生学习其他后续课程（如近世代数、离散数学、计算方法、偏微分方程、泛函分析等）提供基础。在教学方式上，在传统的板书教学中逐渐引入部分章节的多媒体辅助教学方式，鼓励学生学习、并在建模实践中使用数学软件。

二、教学内容

高等代数I

第一章行列式 $\hfill$ 18 学时

§ 1 二阶行列式

§ 2 三阶行列式

§ 3 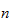阶行列式

§ 4 行列式的展开和转置

§ 5 行列式的计算

§ 6 行列式的等价定义

§ 7 Laplace 定理

本章教学要求：理解和掌握阶行列式的概念，掌握行列式的常用性质和计算方法，并能熟练运用Cramer法则解题。

第二章矩阵 $\hfill$ 10 学时

§ 1 矩阵的概念

§ 2 矩阵的运算

§ 3 矩阵的逆阵

§ 4 矩阵的初等变换与初等矩阵

§ 5 矩阵乘积的行列式与用初等变换法求逆阵

§ 6 分块矩阵

§ 7 Cauchy-Binet公式

本章教学要求：掌握矩阵的运算规律和计算方法，掌握矩阵乘积的行列式定理、可逆矩阵的等价条件，学会运用初等变换计算矩阵的逆阵，学会使用分块矩阵、及Cauchy-Binet公式进行计算。

第三章线性空间 $\hfill$ 30 学时

§ 1 数域

§ 2 行向量和列向量

§ 3 线性空间

§ 4 向量的线性关系

§ 5 向量组的秩

§ 6 矩阵的秩

§ 7 坐标向量

§ 8 基变换与过渡矩阵

§ 9 子空间

§ 10 线性方程组的解

本章教学要求：正确理解抽象的线性空间下定义，掌握线性组合、线性表示、线性相关、线性无关等概念及其相关性质；深刻理解向量组的极大无关组、秩的定义；掌握矩阵的秩与其子式的关系；掌握并能熟练运用基变换与坐标变换的之间关系，掌握子空间概念以及子空间形成直和的条件，掌握子空间和与交的维数公式；正确理解和掌握齐次线性方程组的基础解系, 解空间的维数及与系数矩阵的秩之间的关系；熟练掌握线性方程组的求解理论。

期中考试，考试形式：笔试

第四章线性映射 $\hfill$ 12 学时

§ 1 线性映射的概念

§ 2 线性映射的运算

§ 3 线性映射与矩阵

§ 4 线性映射的像与核

§ 5 不变子空间

\bigskip本章教学要求：理解线性映射的概念，掌握它的运算、性质及在给定基下与矩阵的对应关系，以及在不同基下的矩阵的变化；理解线性映射的像和核的概念及线性变换在不变子空间的扩张基上矩阵的特点。

第五章 $\hfill$ 26 学时

§ 1 一元多项式代数

§ 2 整除

§ 3 最大公因式

§ 4 因式分解

§ 5 多项式函数

§ 6 复系数多项式

§ 7 实系数多项式和有理系数多项式

期末考试，考试形式：笔试

高等代数II

第五章 $\hfill$ 10 学时

§ 8 多元多项式

§ 9 对称多项式

§ 10 结式和判别式

本章教学要求：理解数域上多项式、多项式的整除、最大公因式、不可约多项式、对称多项式、结式的概念，熟练掌握多项式的运算性质、带余除法、辗转相除法；掌握多项式互素的概念和性质、多项式与其导函数的公因式与重因式的联系、代数基本定理及一般数域上多项式的因式分解定理、本原多项式的性质；学会找出有理系数多项式的有理根并能熟练运用Eisenstein判别法。

第六章特征值 $\hfill$ 16 学时

§ 1 特征值和特征向量

§ 2 对角化

§ 3 极小多项式与Cayley-Hamilton定理

§ 4 特征值的估计

本章教学要求：理解和掌握线性变换和矩阵的特征值、特征向量、特征多项式的概念和性质；掌握相似矩阵的特征值、特征向量、特征多项式变化关系；掌握矩阵相似于对角阵的条件；理解最小多项式的概念；掌握Cayley-Hamilton定理和矩阵的最小多项式与其特征多项式、特征值之间关系。

第七章相似标准型 $\hfill$ 26 学时

§ 1 多项式矩阵

§ 2 矩阵的法式

§ 3 不变因子

§ 4 有理标准型

§ 5 初等因子

§ 6 Jordan 标准型

§ 7 Jordan 标准型的进一步讨论和应用举例

§ 8 矩阵函数

本章教学要求：理解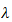 $\lambda$ -矩阵的概念以及数字矩阵相似与其 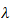$\lambda$ -矩阵相抵的关系；熟练掌握 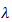$\lambda$ -矩阵的法式、行列式因子及其关系；理解并掌握数字矩阵的不变因子、初等因子、Jordan标准型的概念及其联系，学会计算并运用Jordan标准型讨论矩阵级数等问题。

期中考试，考试形式：笔试

第八章二次型 $\hfill$ 12 学时

§ 1 二次型的化简与矩阵的合同

§ 2 二次型的化简

§ 3 惯性定理

§ 4 正定型与正定矩阵

§ 5 Hermite 型

本章教学要求：理解二次型、二次型与对称矩阵的关系、二次型的标准型和规范型、实对称矩阵的合同等概念；掌握化二次型为规范型的方法、惯性定理；理解正定、半正定、负定二次型（矩阵）的概念；熟练掌握正定法正定矩阵的判别条件，掌握复数域上Hermite 型的概念及计算。

第九章内积空间 $\hfill$ 18 学时

§ 1 内积空间的概念

§ 2 内积的表示和正交基

§ 3 伴随

§ 4 内积空间的同构，正交变换和酉变换

§ 5 自伴随算子

§ 6 复正规矩阵

§ 7 实正规矩阵

§ 8 谱

§ 9 最小二乘解

本章教学要求：理解内积、欧氏（酉）空间的定义及性质；掌握向量的长度，夹角、正交性、标准正交基及基的度量矩阵等概念和相互关系；熟练掌握Gram-Schmidt正交化方法；理解两个欧氏（酉）空间同构、正交（酉）矩阵（变换）、标准正交基之间的联系；掌握正交基扩充定理；掌握自伴随算子与Hermite矩阵的关系；掌握实对称矩阵、实正规矩阵、Hermite矩阵、正规矩阵、酉阵等矩阵集合之间的联系及其正交（酉）相似的对角标准型形式；理解正规矩阵的谱的概念和运算；掌握学会使用矛盾方程组的最小二乘法。

第十章双线性型 $\hfill$ 10 学时

§ 1 对偶空间

§ 2 双线性型

§ 3 纯量积

§ 4 交错型与辛空间

§ 5 对称型与正交几何

本章教学要求：理解对偶空间、双线性型、变换的伴随变换等概念，掌握双线性型与基下矩阵的关系、左右根子空间的概念；理解纯量积的概念以及非退化纯量积下子空间的直和分解性质；掌握（非退化）交错型与辛空间的概念及联系；掌握（非退化）对称型上的正交几何性质。

期末考试，考试形式：笔试

考核方式

闭卷考试

（注：第十章前三节内容必讲，后两节内容选讲）